mempunyai suku konstanta sembarang.
1.2 Rumus-rumus Integral Tak Tentu
1.3 Definisi Integral Tentu
sebagai berikut:
maka menurut dalil pokok dari kalkulus integral, integral tentu diatas dapat dihitung dengan
rumus :
1.4 Rumus-rumus Integral tentu


dengan k sebagai konstanta sembarang.

1.5 Integral Parsial
Prinsip dasar integral parsial :
- Salah satunya dimisalkan U
- Sisinya yang lain (termasuk dx) dianggap sebagai dv
Sehingga bentuk integral parsial adalah sebagai berikut :



1.1 Beberapa Aplikasi dari Integral
a. Perhitungan Luas suatu kurva terhadap sumbu x



b. Menghitung luas diantara dua buah kurva

c. Menghitung volume benda putar yang diputar terhadap sumbu koordinat



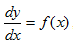




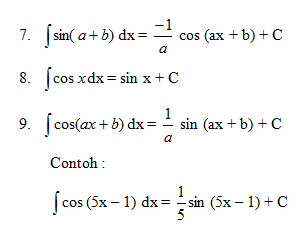



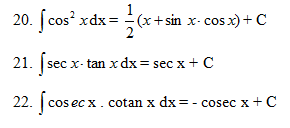

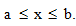





Komentar ini telah dihapus oleh pengarang.
BalasHapusassalamualaikum warahmatullahi wabarakatu....................................
BalasHapustolong anda berikan contoh dari integral tak tentu dan integral tentu
tolong dijawab 32x dx
BalasHapustolong dijawab 32x dx
BalasHapus∫▒〖32 x dx= 32/(1+1) x^(1+1)+C 〗
Hapus=(32 )/2 x^2+C
=16 x^2+C
terimakasih ilmunya
BalasHapusterimakasih ilmunya
BalasHapusWorthy bnget kak
BalasHapusTolong jawab integral (2x-3) dx
BalasHapusx²-3x+c
HapusKalo y2 = 9x dan x'2= 9y.gimana
BalasHapusTolong di jawab..
BalasHapus(X^4+3X^2+1)^8(4X^3+6X)dx
Jelaskan langkahnya juga yea...
HapusPusing sya 😨
BalasHapusSabarrr kwkwkwkw
BalasHapusIntegral tak tentu dari ∫8^2x
BalasHapus3xkuadrat3 -5x+3
BalasHapus2xkuadrat2
Komentar ini telah dihapus oleh pengarang.
Hapus4x2-2cosx+3ex dx
BalasHapus